Examples of benchmarks

The following figures are examples of algorithm benchmarks which can be generated very easily from the platform In all examples, we use independent experiments for the different x-values; so that consistent rankings between methods, over several x-values, have a statistical meaning.

If you want to run the examples yourself, please make sure you have installed nevergrad with the benchmark flag (see here).

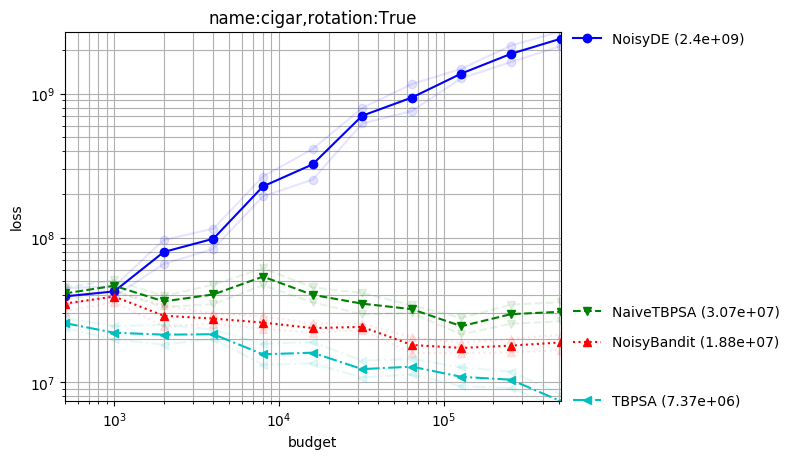
Noisy optimization

Created with command:

python -m nevergrad.benchmark noise --seed=12 --repetitions=10 --plot

Here the variance of the noise does not vanish near the optimum. TBPSA uses the noise management principles of pcCMSA-ES reaching fast convergence rates. We here compare it to a sample of our algorithms; but it performed very well also compared to many other methods.

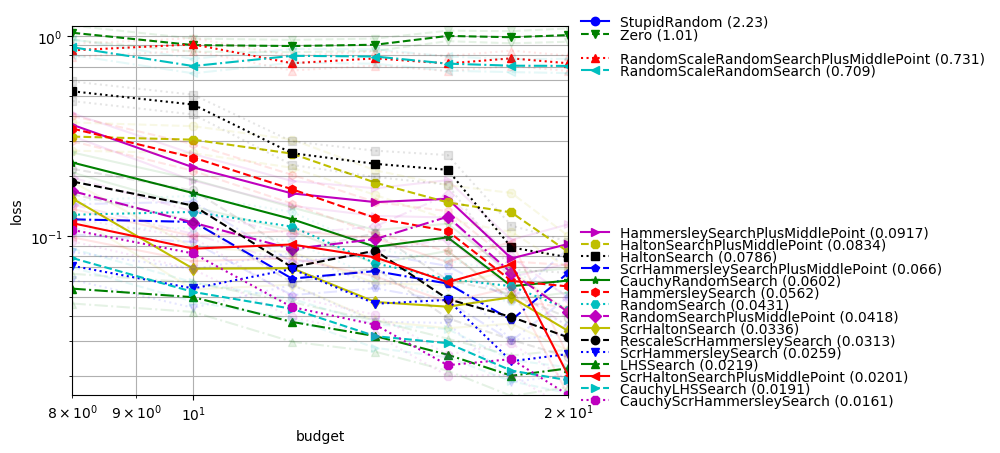
One-shot optimization

In dimension-11 with one feature

Created with command:

python -m nevergrad.benchmark dim10_select_one_feature --seed=12 --repetitions=400 --plot

One-shot optimization is the case in which all evaluations should be done in parallel; the optimization algorithm can only decide, once and for all, which points are going to be evaluated. We consider here:

• an optimum which is translated by a standard centered Gaussian;

• 1 useful variable and 10 useless variables (this is a feature selection context as in https://arxiv.org/abs/1706.03200);

• the sphere function (restricted to the useful variable);

We see that:

• Quasirandom without scrambling is suboptimal;

• Cauchy sampling helps a lot (though the optimum is normally drawn!), in this feature selection context;

• LHS performs equivalently to low discrepancy (which can be related to the fact that only one feature matters).

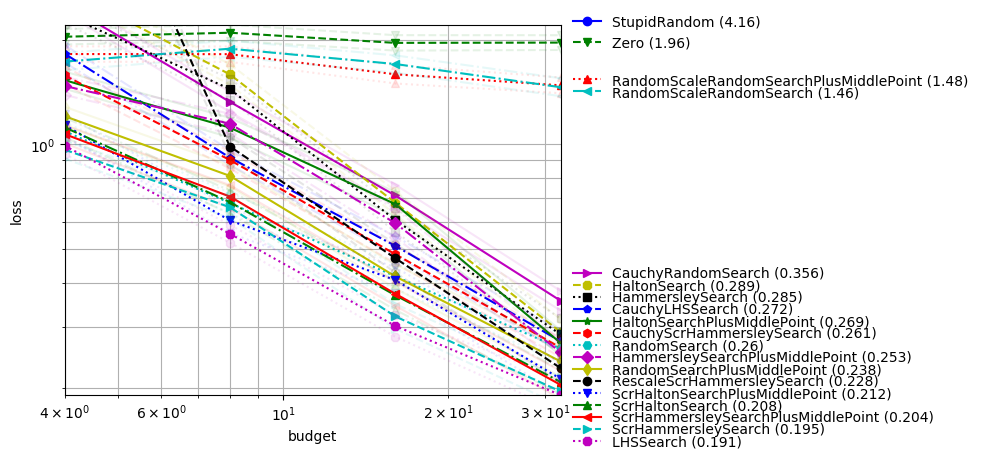
In dimension-12 with two features

We reproduce this experiment but with 2 useful variables:

python -m nevergrad.benchmark dim10_select_two_features --seed=12 --repetitions=400 --plot

LHS still performs very well, as well as scrambled methods; Cauchy is not that useful anymore.

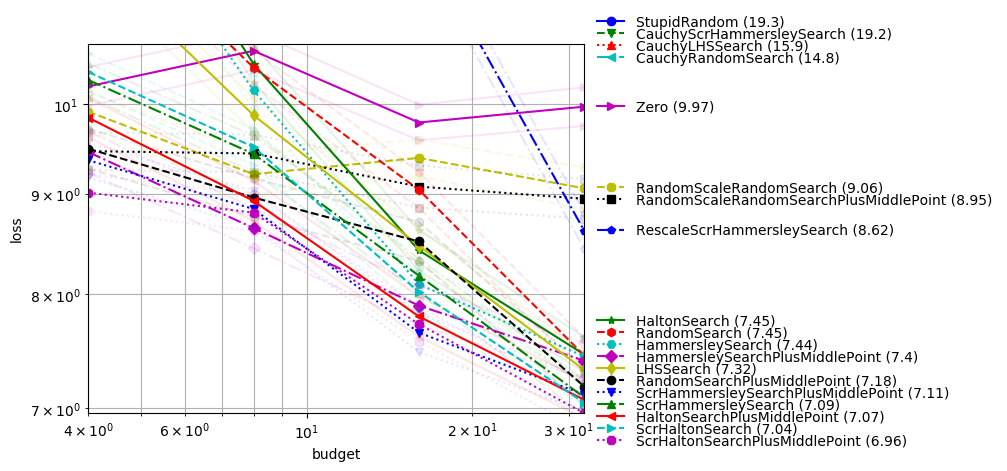
In dimension-10 with small budget

With all variables useful, the situation becomes different; Cauchy is harmful. Scrambling is still very necessary. LHS (vanilla), which does not couple variables, is weak.

python -m nevergrad.benchmark dim10_smallbudget --seed=12 --repetitions=400 --plot

In dimension-4

In moderate dimension, scrambling is less necessary (consistently with theory) and LHS becomes weaker as budget increases (consistently with discrepancy results in https://arxiv.org/abs/1707.08481). The following plot was created with command:

python -m nevergrad.benchmark doe_dim4 --seed=12 --repetitions=400 --plot

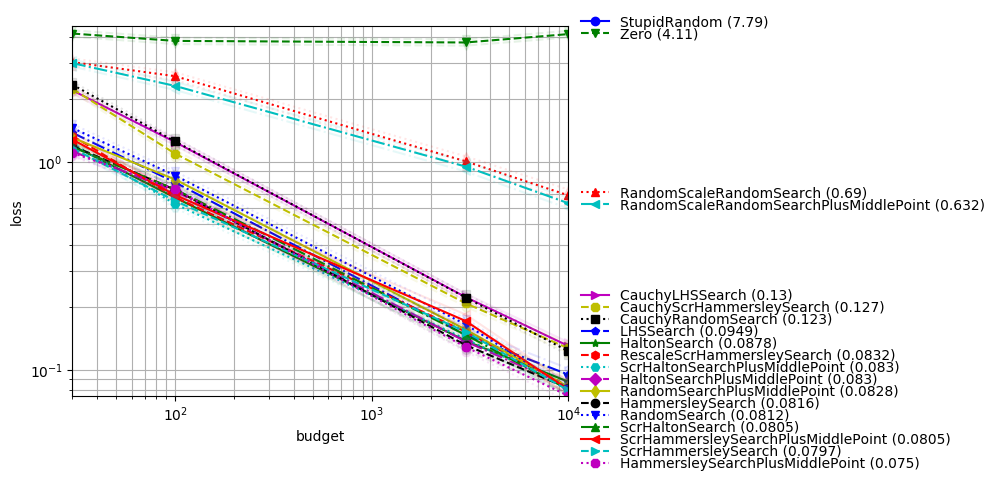
Comparison-based methods for ill-conditioned problems

In this setting (rotated or not, ill-conditioned) we get excellent results with:

• CMA, best on the Cigar and rotated ellipsoid;

• DE and PSO when there is no rotation;

• Almost rotationally invariant variants of DE in the rotated case (CR should not be exactly equal to 1, otherwise we stay in the vector space generated by the initial population; this confirms results and explanation in http://users.cecs.anu.edu.au/~ejmontgomery/publications/2010-07_de_cr_moves.pdf);

python -m nevergrad.benchmark compabasedillcond --seed=12 --repetitions=400 --plot

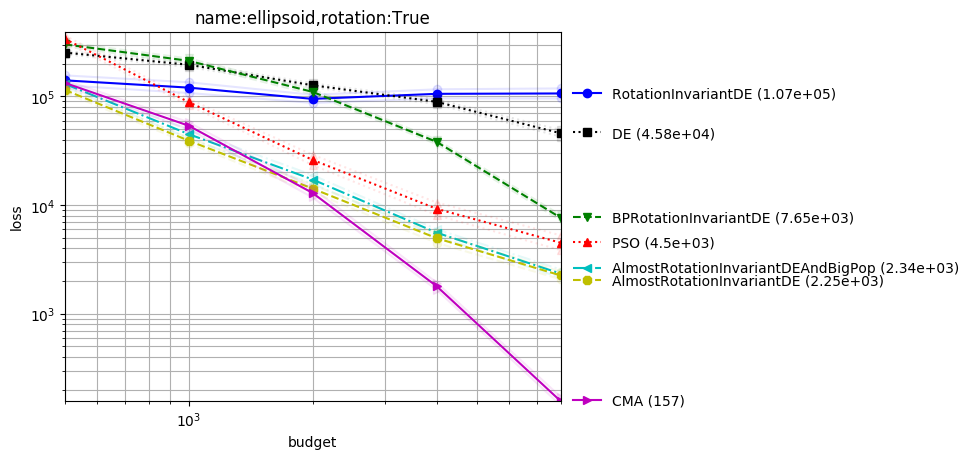
Ill-conditioned function

SQP (which won the BBComp GECCO 2015 contest) performs great in the quadratic case, consistently with theory and intuition:

python -m nevergrad.benchmark illcond --seed=12 --repetitions=50 --plot

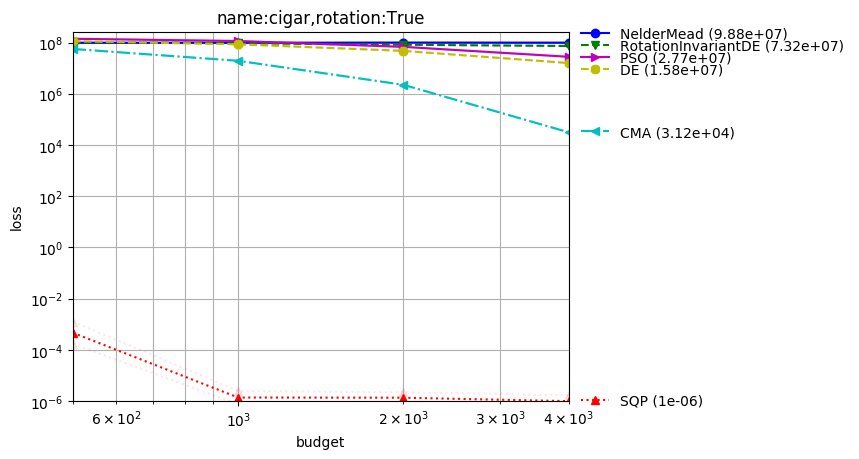
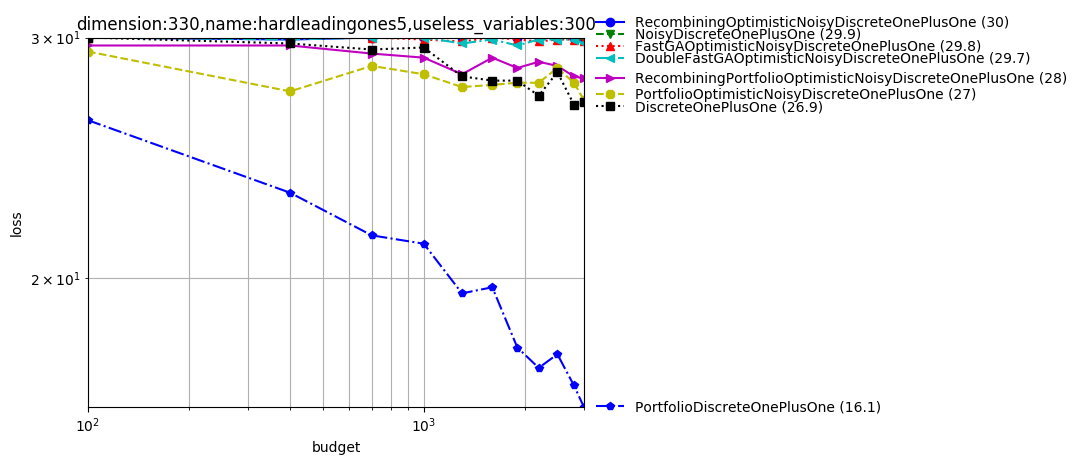
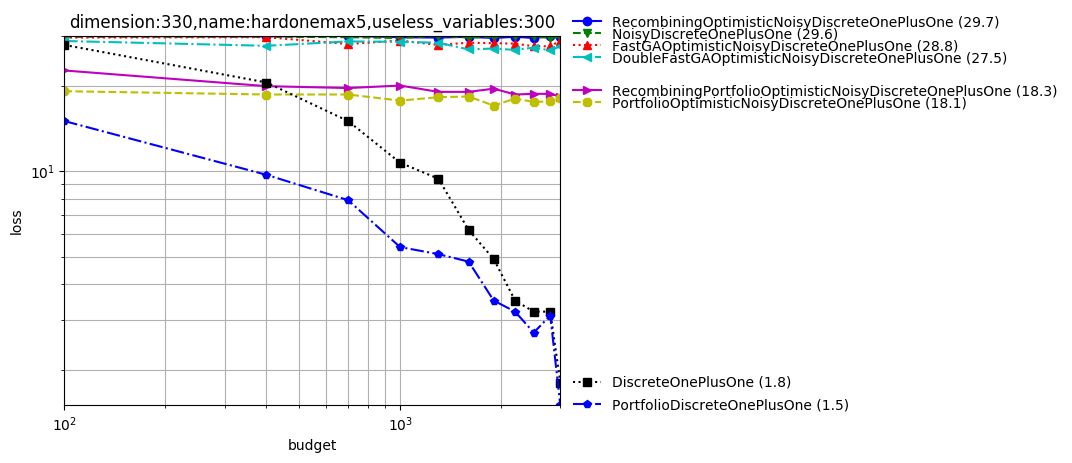
Discrete

The platform can also deal with discrete objective functions! We can both consider discrete domains handled through softmax or through discretization of continuous variables.

python -m nevergrad.benchmark discrete --seed=12 --repetitions=10 --plot

We note that FastGA performs best. DoubleFastGA corresponds to a mutation rate ranging between 1/dim and (dim-1)/dim instead of 1/dim and 1/2; this is because the original range corresponds to a binary domain whereas we consider arbitrary domains. The simple uniform mixing of mutation rates (https://arxiv.org/abs/1606.05551) performs well in several cases.

List of benchmarks

You can find a list of currently available benchmarks below. Most are not well-documented, please open an issue when you need more information and we’ll update the documentation on demand ;)

nevergrad.benchmark.frozenexperiments.basic(seed: Optional[int] = None) → Iterator[Experiment]

Test settings

nevergrad.benchmark.frozenexperiments.compabasedillcond(seed: Optional[int] = None) → Iterator[Experiment]

All optimizers on ill cond problems

nevergrad.benchmark.frozenexperiments.dim10_select_one_feature(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.frozenexperiments.dim10_select_two_features(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.frozenexperiments.dim10_smallbudget(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.frozenexperiments.doe_dim4(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.frozenexperiments.illcond(seed: Optional[int] = None) → Iterator[Experiment]

All optimizers on ill cond problems

nevergrad.benchmark.frozenexperiments.metanoise(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.frozenexperiments.noise(seed: Optional[int] = None) → Iterator[Experiment]

All optimizers on ill cond problems

nevergrad.benchmark.frozenexperiments.oneshot1(seed: Optional[int] = None) → Iterator[Experiment]

Comparing one-shot optimizers as initializers for Bayesian Optimization.

nevergrad.benchmark.frozenexperiments.oneshot2(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.frozenexperiments.oneshot3(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.frozenexperiments.oneshot4(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.frozenexperiments.repeated_basic(seed: Optional[int] = None) → Iterator[Experiment]

Test settings

nevergrad.benchmark.experiments.adversarial_attack(seed: Optional[int] = None) → Iterator[Experiment]

Pretrained ResNes50 under black-box attacked. Square attacks: 100 queries ==> 0.1743119266055046 200 queries ==> 0.09043250327653997 300 queries ==> 0.05111402359108781 400 queries ==> 0.04325032765399738 1700 queries ==> 0.001310615989515072

nevergrad.benchmark.experiments.alldes(seed: Optional[int] = None) → Iterator[Experiment]

All DE methods on various functions. Dimension 5, 20, 100. Sphere, Cigar, Hm, Ellipsoid. Budget 10, 100, 1000, 10000, 100000.

nevergrad.benchmark.experiments.aquacrop_fao(seed: Optional[int] = None) → Iterator[Experiment]

FAO Crop simulator. Maximize yield.

nevergrad.benchmark.experiments.bonnans(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.experiments.causal_similarity(seed: Optional[int] = None) → Iterator[Experiment]

Finding the best causal graph

nevergrad.benchmark.experiments.ceviche(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.experiments.complex_tsp(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of simple_tsp with non-planar term.

nevergrad.benchmark.experiments.constrained_illconditioned_parallel(seed: Optional[int] = None) → Iterator[Experiment]

Many optimizers on ill cond problems with constraints.

nevergrad.benchmark.experiments.control_problem(seed: Optional[int] = None) → Iterator[Experiment]

MuJoCo testbed. Learn linear policy for different control problems. Budget 500, 1000, 3000, 5000.

nevergrad.benchmark.experiments.deceptive(seed: Optional[int] = None) → Iterator[Experiment]

Very difficult objective functions: one is highly multimodal (infinitely many local optima), one has an infinite condition number, one has an infinitely long path towards the optimum. Looks somehow fractal.

nevergrad.benchmark.experiments.doe(seed: Optional[int] = None) → Iterator[Experiment]

One shot optimization of 3 classical objective functions (sphere, rastrigin, cigar), simplified. Base dimension 2000 or 20000. No rotation, no dummy variable. Budget 30, 100, 3000, 10000, 30000, 100000.

nevergrad.benchmark.experiments.double_o_seven(seed: Optional[int] = None) → Iterator[Experiment]

Optimization of policies for the 007 game. Sequential or 10-parallel or 100-parallel. Various numbers of averagings: 1, 10 or 100.

nevergrad.benchmark.experiments.far_optimum_es(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.experiments.fishing(seed: Optional[int] = None) → Iterator[Experiment]

Lotka-Volterra equations

nevergrad.benchmark.experiments.fiveshots(seed: Optional[int] = None) → Iterator[Experiment]

Five-shots optimization of 3 classical objective functions (sphere, rastrigin, cigar). Base dimension 3 or 25. 0 or 5 dummy variable per real variable. Budget 30, 100 or 3000.

nevergrad.benchmark.experiments.harderparallel(seed: Optional[int] = None) → Iterator[Experiment]

Parallel optimization on 4 classical objective functions. More distinct settings than << parallel >>.

nevergrad.benchmark.experiments.hdbo4d(seed: Optional[int] = None) → Iterator[Experiment]

All Bayesian optimization methods on various functions. Budget 25, 31, 37, 43, 50, 60. Dimension 20. Sphere, Cigar, Hm, Ellipsoid.

nevergrad.benchmark.experiments.hdmultimodal(seed: Optional[int] = None) → Iterator[Experiment]

Experiment on multimodal functions, namely hm, rastrigin, griewank, rosenbrock, ackley, lunacek, deceptivemultimodal. Similar to multimodal, but dimension 20 or 100 or 1000. Budget 1000 or 10000, sequential.

nevergrad.benchmark.experiments.illcondi(seed: Optional[int] = None) → Iterator[Experiment]

Testing optimizers on ill cond problems. Cigar, Ellipsoid. Both rotated and unrotated. Budget 100, 1000, 10000. Dimension 50.

nevergrad.benchmark.experiments.illcondipara(seed: Optional[int] = None) → Iterator[Experiment]

Testing optimizers on ill-conditionned parallel optimization. 50 workers in parallel.

nevergrad.benchmark.experiments.image_multi_similarity(seed: Optional[int] = None, cross_valid: bool = False, with_pgan: bool = False) → Iterator[Experiment]

Optimizing images: artificial criterion for now.

nevergrad.benchmark.experiments.image_multi_similarity_cv(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of image_multi_similarity with cross-validation.

nevergrad.benchmark.experiments.image_multi_similarity_pgan(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of image_similarity, using PGan as a representation.

nevergrad.benchmark.experiments.image_multi_similarity_pgan_cv(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of image_multi_similarity with cross-validation.

nevergrad.benchmark.experiments.image_quality(seed: Optional[int] = None, cross_val: bool = False, with_pgan: bool = False, num_images: int = 1) → Iterator[Experiment]

Optimizing images for quality: we optimize K512, Blur and Brisque.

With num_images > 1, we are doing morphing.

nevergrad.benchmark.experiments.image_quality_cv(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of image_quality with cross-validation.

nevergrad.benchmark.experiments.image_quality_cv_pgan(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of image_quality with cross-validation.

nevergrad.benchmark.experiments.image_quality_pgan(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of image_quality with cross-validation.

nevergrad.benchmark.experiments.image_quality_proxy(seed: Optional[int] = None, with_pgan: bool = False) → Iterator[Experiment]

Optimizing images: artificial criterion for now.

nevergrad.benchmark.experiments.image_quality_proxy_pgan(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.experiments.image_similarity(seed: Optional[int] = None, with_pgan: bool = False, similarity: bool = True) → Iterator[Experiment]

Optimizing images: artificial criterion for now.

nevergrad.benchmark.experiments.image_similarity_and_quality(seed: Optional[int] = None, cross_val: bool = False, with_pgan: bool = False) → Iterator[Experiment]

Optimizing images: artificial criterion for now.

nevergrad.benchmark.experiments.image_similarity_and_quality_cv(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of image_similarity_and_quality with cross-validation.

nevergrad.benchmark.experiments.image_similarity_and_quality_cv_pgan(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of image_similarity_and_quality with cross-validation.

nevergrad.benchmark.experiments.image_similarity_and_quality_pgan(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of image_similarity_and_quality with cross-validation.

nevergrad.benchmark.experiments.image_similarity_pgan(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of image_similarity, using PGan as a representation.

nevergrad.benchmark.experiments.image_single_quality(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of image_similarity, but based on image quality assessment.

nevergrad.benchmark.experiments.image_single_quality_pgan(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of image_similarity_pgan, but based on image quality assessment.

nevergrad.benchmark.experiments.instrum_discrete(seed: Optional[int] = None) → Iterator[Experiment]

Comparison of optimization algorithms equipped with distinct instrumentations. Onemax, Leadingones, Jump function.

nevergrad.benchmark.experiments.keras_tuning(seed: Optional[int] = None, overfitter: bool = False, seq: bool = False, veryseq: bool = False) → Iterator[Experiment]

Machine learning hyperparameter tuning experiment. Based on Keras models.

nevergrad.benchmark.experiments.lowbudget(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.experiments.lsgo() → Iterator[Experiment]

nevergrad.benchmark.experiments.mixsimulator(seed: Optional[int] = None) → Iterator[Experiment]

MixSimulator of power plants Budget 20, 40, …, 1600. Sequential or 30 workers.

nevergrad.benchmark.experiments.mlda(seed: Optional[int] = None) → Iterator[Experiment]

MLDA (machine learning and data analysis) testbed.

nevergrad.benchmark.experiments.mldakmeans(seed: Optional[int] = None) → Iterator[Experiment]

MLDA (machine learning and data analysis) testbed, restricted to the K-means part.

nevergrad.benchmark.experiments.mltuning(seed: Optional[int] = None, overfitter: bool = False, seq: bool = False, veryseq: bool = False, nano: bool = False) → Iterator[Experiment]

Machine learning hyperparameter tuning experiment. Based on scikit models.

nevergrad.benchmark.experiments.mono_rocket(seed: Optional[int] = None) → Iterator[Experiment]

Sequential counterpart of the rocket problem.

nevergrad.benchmark.experiments.morphing_pgan_quality(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.experiments.ms_bbob(seed: Optional[int] = None) → Iterator[Experiment]

Testing optimizers on exponentiated problems. Cigar, Ellipsoid. Both rotated and unrotated. Budget 100, 1000, 10000. Dimension 50.

nevergrad.benchmark.experiments.multi_ceviche(seed: Optional[int] = None, c0: bool = False, precompute: bool = False, warmstart: bool = False) → Iterator[Experiment]

Categories when running with c0: BFGScheat works on the continuous problem, with continuous domain, with continuous test. BFGS works on the continuous problem, with continuous domain, with discrete test. Alg+C0 works on the continuous problem, with continuous domain, with discrete test. Alg+C0C works on the continuous problem, with continuous domain, with continuous test. Alg+C0p works on the continuous problem, with continuous domain, with discrete test. Penalization. Alg works on the discrete problem on a discrete domain. For each Alg in Nevergrad optimizers listed below.

Please launch the experiment command multiple times: python -m nevergrad.benchmark multi_ceviche_c0

nevergrad.benchmark.experiments.multi_ceviche_c0(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of multi_ceviche with continuous permittivities.

nevergrad.benchmark.experiments.multi_ceviche_c0_warmstart(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of multi_ceviche with continuous permittivities.

nevergrad.benchmark.experiments.multi_ceviche_c0p(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of multi_ceviche with continuous permittivities and warmstart.

nevergrad.benchmark.experiments.multimodal(seed: Optional[int] = None, para: bool = False) → Iterator[Experiment]

Experiment on multimodal functions, namely hm, rastrigin, griewank, rosenbrock, ackley, lunacek, deceptivemultimodal. 0 or 5 dummy variable per real variable. Base dimension 3 or 25. Budget in 3000, 10000, 30000, 100000. Sequential.

nevergrad.benchmark.experiments.multiobjective_example(seed: Optional[int] = None, hd: bool = False, many: bool = False) → Iterator[Experiment]

Optimization of 2 and 3 objective functions in Sphere, Ellipsoid, Cigar, Hm. Dimension 6 and 7. Budget 100 to 3200

nevergrad.benchmark.experiments.multiobjective_example_hd(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of moo with high dimension.

nevergrad.benchmark.experiments.multiobjective_example_many(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of moo with more objective functions.

nevergrad.benchmark.experiments.multiobjective_example_many_hd(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of moo with high dimension and more objective functions.

nevergrad.benchmark.experiments.naive_seq_keras_tuning(seed: Optional[int] = None) → Iterator[Experiment]

Naive counterpart (no overfitting, see naivemltuning)of seq_keras_tuning.

nevergrad.benchmark.experiments.naive_seq_mltuning(seed: Optional[int] = None) → Iterator[Experiment]

Iterative counterpart of mltuning with overfitting of valid loss, i.e. train/valid/valid instead of train/valid/test.

nevergrad.benchmark.experiments.naive_veryseq_keras_tuning(seed: Optional[int] = None) → Iterator[Experiment]

Naive counterpart (no overfitting, see naivemltuning)of seq_keras_tuning.

nevergrad.benchmark.experiments.naivemltuning(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of mltuning with overfitting of valid loss, i.e. train/valid/valid instead of train/valid/test.

nevergrad.benchmark.experiments.nano_naive_seq_mltuning(seed: Optional[int] = None) → Iterator[Experiment]

Iterative counterpart of mltuning with overfitting of valid loss, i.e. train/valid/valid instead of train/valid/test, and with lower budget.

nevergrad.benchmark.experiments.nano_naive_veryseq_mltuning(seed: Optional[int] = None) → Iterator[Experiment]

Iterative counterpart of mltuning with overfitting of valid loss, i.e. train/valid/valid instead of train/valid/test, and with lower budget.

nevergrad.benchmark.experiments.nano_seq_mltuning(seed: Optional[int] = None) → Iterator[Experiment]

Iterative counterpart of seq_mltuning with smaller budget.

nevergrad.benchmark.experiments.nano_veryseq_mltuning(seed: Optional[int] = None) → Iterator[Experiment]

Iterative counterpart of seq_mltuning with smaller budget.

nevergrad.benchmark.experiments.neuro_control_problem(seed: Optional[int] = None) → Iterator[Experiment]

MuJoCo testbed. Learn neural policies.

nevergrad.benchmark.experiments.newdoe(seed: Optional[int] = None) → Iterator[Experiment]

One shot optimization of 3 classical objective functions (sphere, rastrigin, cigar), simplified. Tested on more dimensionalities than doe, namely 20, 200, 2000, 20000. No dummy variables. Budgets 30, 100, 3000, 10000, 30000, 100000, 300000.

nevergrad.benchmark.experiments.noisy(seed: Optional[int] = None) → Iterator[Experiment]

Noisy optimization methods on a few noisy problems. Sphere, Rosenbrock, Cigar, Hm (= highly multimodal). Noise level 10. Noise dyssymmetry or not. Dimension 2, 20, 200, 2000. Budget 25000, 50000, 100000.

nevergrad.benchmark.experiments.nozp_noms_bbob(seed: Optional[int] = None) → Iterator[Experiment]

Testing optimizers on exponentiated problems. Cigar, Ellipsoid. Both rotated and unrotated. Budget 100, 1000, 10000. Dimension 50.

nevergrad.benchmark.experiments.olympus_emulators(seed: Optional[int] = None) → Iterator[Experiment]

Olympus emulators

nevergrad.benchmark.experiments.olympus_surfaces(seed: Optional[int] = None) → Iterator[Experiment]

Olympus surfaces

nevergrad.benchmark.experiments.oneshot(seed: Optional[int] = None) → Iterator[Experiment]

One shot optimization of 3 classical objective functions (sphere, rastrigin, cigar). 0 or 5 dummy variables per real variable. Base dimension 3 or 25. budget 30, 100 or 3000.

nevergrad.benchmark.experiments.oneshot_mltuning(seed: Optional[int] = None) → Iterator[Experiment]

One-shot counterpart of Scikit tuning.

nevergrad.benchmark.experiments.paraalldes(seed: Optional[int] = None) → Iterator[Experiment]

All DE methods on various functions. Parallel version. Dimension 5, 20, 100, 500, 2500. Sphere, Cigar, Hm, Ellipsoid. No rotation.

nevergrad.benchmark.experiments.parahdbo4d(seed: Optional[int] = None) → Iterator[Experiment]

All Bayesian optimization methods on various functions. Parallel version Dimension 20 and 2000. Budget 25, 31, 37, 43, 50, 60. Sphere, Cigar, Hm, Ellipsoid. No rotation.

nevergrad.benchmark.experiments.parallel(seed: Optional[int] = None) → Iterator[Experiment]

Parallel optimization on 3 classical objective functions: sphere, rastrigin, cigar. The number of workers is 20 % of the budget. Testing both no useless variables and 5/6 of useless variables.

nevergrad.benchmark.experiments.parallel_small_budget(seed: Optional[int] = None) → Iterator[Experiment]

Parallel optimization with small budgets

nevergrad.benchmark.experiments.paramultimodal(seed: Optional[int] = None) → Iterator[Experiment]

Parallel counterpart of the multimodal experiment: 1000 workers.

nevergrad.benchmark.experiments.pbbob(seed: Optional[int] = None) → Iterator[Experiment]

Testing optimizers on exponentiated problems. Cigar, Ellipsoid. Both rotated and unrotated. Budget 100, 1000, 10000. Dimension 50.

nevergrad.benchmark.experiments.pbo_reduced_suite(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.experiments.pbo_suite(seed: Optional[int] = None, reduced: bool = False) → Iterator[Experiment]

nevergrad.benchmark.experiments.pbt(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.experiments.photonics(seed: Optional[int] = None, as_tuple: bool = False, small: bool = False, ultrasmall: bool = False, verysmall: bool = False) → Iterator[Experiment]

Too small for being interesting: Bragg mirror + Chirped + Morpho butterfly.

nevergrad.benchmark.experiments.photonics2(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with higher dimensions.

nevergrad.benchmark.experiments.powersystems(seed: Optional[int] = None) → Iterator[Experiment]

Unit commitment problem, i.e. management of dams for hydroelectric planning.

nevergrad.benchmark.experiments.ranknoisy(seed: Optional[int] = None) → Iterator[Experiment]

Noisy optimization methods on a few noisy problems. Cigar, Altcigar, Ellipsoid, Altellipsoid. Dimension 200, 2000, 20000. Budget 25000, 50000, 100000. No rotation. Noise level 10. With or without noise dissymmetry.

nevergrad.benchmark.experiments.realworld(seed: Optional[int] = None) → Iterator[Experiment]

Realworld optimization. This experiment contains:

• a subset of MLDA (excluding the perceptron: 10 functions rescaled or not.

• ARCoating https://arxiv.org/abs/1904.02907: 1 function.

• The 007 game: 1 function, noisy.

• PowerSystem: a power system simulation problem.

• STSP: a simple TSP problem.

• MLDA, except the Perceptron.

Budget 25, 50, 100, 200, 400, 800, 1600, 3200, 6400, 12800. Sequential or 10-parallel or 100-parallel.

nevergrad.benchmark.experiments.reduced_yahdlbbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with HD and low budget.

nevergrad.benchmark.experiments.refactor_optims(x: List[Any]) → List[Any]

nevergrad.benchmark.experiments.rocket(seed: Optional[int] = None, seq: bool = False) → Iterator[Experiment]

Rocket simulator. Maximize max altitude by choosing the thrust schedule, given a total thrust. Budget 25, 50, …, 1600. Sequential or 30 workers.

nevergrad.benchmark.experiments.seq_keras_tuning(seed: Optional[int] = None) → Iterator[Experiment]

Iterative counterpart of keras tuning.

nevergrad.benchmark.experiments.seq_mltuning(seed: Optional[int] = None) → Iterator[Experiment]

Iterative counterpart of mltuning.

nevergrad.benchmark.experiments.sequential_fastgames(seed: Optional[int] = None) → Iterator[Experiment]

Optimization of policies for games, i.e. direct policy search. Budget 12800, 25600, 51200, 102400. Games: War, Batawaf, Flip, GuessWho, BigGuessWho.

nevergrad.benchmark.experiments.sequential_instrum_discrete(seed: Optional[int] = None) → Iterator[Experiment]

Sequential counterpart of instrum_discrete.

nevergrad.benchmark.experiments.sequential_topology_optimization(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.experiments.simple_tsp(seed: Optional[int] = None, complex_tsp: bool = False) → Iterator[Experiment]

Simple TSP problems. Please note that the methods we use could be applied or complex variants, whereas specialized methods can not always do it; therefore this comparisons from a black-box point of view makes sense even if white-box methods are not included though they could do this more efficiently. 10, 100, 1000, 10000 cities. Budgets doubling from 25, 50, 100, 200, … up to 25600

nevergrad.benchmark.experiments.skip_ci(*, reason: str) → None

Only use this if there is a good reason for not testing the xp, such as very slow for instance (>1min) with no way to make it faster. This is dangereous because it won’t test reproducibility and the experiment may therefore be corrupted with no way to notice it automatically.

nevergrad.benchmark.experiments.small_photonics(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with higher dimensions.

nevergrad.benchmark.experiments.small_photonics2(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with higher dimensions.

nevergrad.benchmark.experiments.smallbudget_lsgo() → Iterator[Experiment]

nevergrad.benchmark.experiments.spsa_benchmark(seed: Optional[int] = None) → Iterator[Experiment]

Some optimizers on a noisy optimization problem. This benchmark is based on the noisy benchmark. Budget 500, 1000, 2000, 4000, … doubling… 128000. Rotation or not. Sphere, Sphere4, Cigar.

nevergrad.benchmark.experiments.team_cycling(seed: Optional[int] = None) → Iterator[Experiment]

Experiment to optimise team pursuit track cycling problem.

nevergrad.benchmark.experiments.topology_optimization(seed: Optional[int] = None) → Iterator[Experiment]

nevergrad.benchmark.experiments.ultrasmall_photonics(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with higher dimensions.

nevergrad.benchmark.experiments.ultrasmall_photonics2(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with higher dimensions.

nevergrad.benchmark.experiments.unit_commitment(seed: Optional[int] = None) → Iterator[Experiment]

Unit commitment problem.

nevergrad.benchmark.experiments.veryseq_keras_tuning(seed: Optional[int] = None) → Iterator[Experiment]

Iterative counterpart of keras tuning.

nevergrad.benchmark.experiments.verysmall_photonics(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with higher dimensions.

nevergrad.benchmark.experiments.verysmall_photonics2(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with higher dimensions.

nevergrad.benchmark.experiments.yabbob(seed: Optional[int] = None, parallel: bool = False, big: bool = False, small: bool = False, noise: bool = False, hd: bool = False, constraint_case: int = 0, split: bool = False, tuning: bool = False, reduction_factor: int = 1, bounded: bool = False, box: bool = False, max_num_constraints: int = 4, mega_smooth_penalization: int = 0) → Iterator[Experiment]

Yet Another Black-Box Optimization Benchmark. Related to, but without special effort for exactly sticking to, the BBOB/COCO dataset. Dimension 2, 10 and 50. Budget 50, 200, 800, 3200, 12800. Both rotated or not rotated.

nevergrad.benchmark.experiments.yabigbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with more budget.

nevergrad.benchmark.experiments.yaboundedbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with bounded domain and dim only 40, (-5,5)**n by default.

nevergrad.benchmark.experiments.yaboxbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with bounded domain, (-5,5)**n by default.

nevergrad.benchmark.experiments.yaconstrainedbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with constraints. Constraints are cheap: we do not count calls to them.

nevergrad.benchmark.experiments.yahdbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with higher dimensions.

nevergrad.benchmark.experiments.yahdlbbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with HD and low budget.

nevergrad.benchmark.experiments.yahdnoisybbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with higher dimensions.

nevergrad.benchmark.experiments.yahdnoisysplitbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with more budget.

nevergrad.benchmark.experiments.yahdsplitbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yasplitbbob with more dimension.

nevergrad.benchmark.experiments.yamegapenbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with penalized constraints.

nevergrad.benchmark.experiments.yamegapenbigbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with penalized constraints.

nevergrad.benchmark.experiments.yamegapenboundedbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with penalized constraints.

nevergrad.benchmark.experiments.yamegapenboxbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with penalized constraints.

nevergrad.benchmark.experiments.yamegapenhdbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with penalized constraints.

nevergrad.benchmark.experiments.yanoisybbob(seed: Optional[int] = None) → Iterator[Experiment]

Noisy optimization counterpart of yabbob. This is supposed to be consistent with normal practices in noisy optimization: we distinguish recommendations and exploration. This is different from the original BBOB/COCO from that point of view.

nevergrad.benchmark.experiments.yanoisysplitbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with more budget.

nevergrad.benchmark.experiments.yaonepenbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with penalized constraints.

nevergrad.benchmark.experiments.yaonepenbigbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with penalized constraints.

nevergrad.benchmark.experiments.yaonepenboundedbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabooundedbbob with penalized constraints.

nevergrad.benchmark.experiments.yaonepenboxbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yaboxbbob with penalized constraints.

nevergrad.benchmark.experiments.yaonepennoisybbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yanoisybbob with penalized constraints.

nevergrad.benchmark.experiments.yaonepenparabbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yaparabbob with penalized constraints.

nevergrad.benchmark.experiments.yaonepensmallbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yasmallbbob with penalized constraints.

nevergrad.benchmark.experiments.yaparabbob(seed: Optional[int] = None) → Iterator[Experiment]

Parallel optimization counterpart of yabbob.

nevergrad.benchmark.experiments.yapenbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with penalized constraints.

nevergrad.benchmark.experiments.yapenboundedbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabooundedbbob with penalized constraints.

nevergrad.benchmark.experiments.yapenboxbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yaboxbbob with penalized constraints.

nevergrad.benchmark.experiments.yapennoisybbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yanoisybbob with penalized constraints.

nevergrad.benchmark.experiments.yapenparabbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yaparabbob with penalized constraints.

nevergrad.benchmark.experiments.yapensmallbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yasmallbbob with penalized constraints.

nevergrad.benchmark.experiments.yasmallbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with less budget.

nevergrad.benchmark.experiments.yasplitbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with splitting info in the instrumentation.

nevergrad.benchmark.experiments.yatinybbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with less budget and less xps.

nevergrad.benchmark.experiments.yatuningbbob(seed: Optional[int] = None) → Iterator[Experiment]

Counterpart of yabbob with less budget and less dimension.

nevergrad.benchmark.experiments.yawidebbob(seed: Optional[int] = None) → Iterator[Experiment]

Yet Another Wide Black-Box Optimization Benchmark. The goal is basically to have a very wide family of problems: continuous and discrete, noisy and noise-free, mono- and multi-objective, constrained and not constrained, sequential and parallel.

TODO(oteytaud): this requires a significant improvement, covering mixed problems and different types of constraints.

nevergrad.benchmark.experiments.zp_ms_bbob(seed: Optional[int] = None) → Iterator[Experiment]

Testing optimizers on exponentiated problems. Cigar, Ellipsoid. Both rotated and unrotated. Budget 100, 1000, 10000. Dimension 50.

nevergrad.benchmark.experiments.zp_pbbob(seed: Optional[int] = None) → Iterator[Experiment]

Testing optimizers on exponentiated problems. Cigar, Ellipsoid. Both rotated and unrotated. Budget 100, 1000, 10000. Dimension 50.