Skip to main content

Transformations

Ocean provides a comprehensive suite of tools for computing geometric transformations between images and point sets. These transformations are essential for image alignment, 3D reconstruction, augmented reality, motion tracking, and sensor fusion.

Overview​

Geometric transformations describe how points in one coordinate system map to another. Ocean supports several transformation types, each with different degrees of freedom (DOF) and properties. Choosing the right transformation depends on your application's requirements.

Transformation Comparison​

TransformationDOFMin PointsProperties PreservedUse Cases
Homography84Straight lines, cross-ratioImage stitching, perspective correction, AR overlays
Affine63Parallel lines, area ratiosTexture mapping, shear correction
Similarity42Shape (angles, proportions)Logo placement, shape-preserving scaling
Homothetic32Orientation, shapeSimple positioning and uniform scaling
Absolute6-73Structure (3D)SLAM, sensor fusion, multi-view alignment

Transformation Hierarchy​

The 2D transformations form a hierarchy where each level adds restrictions:

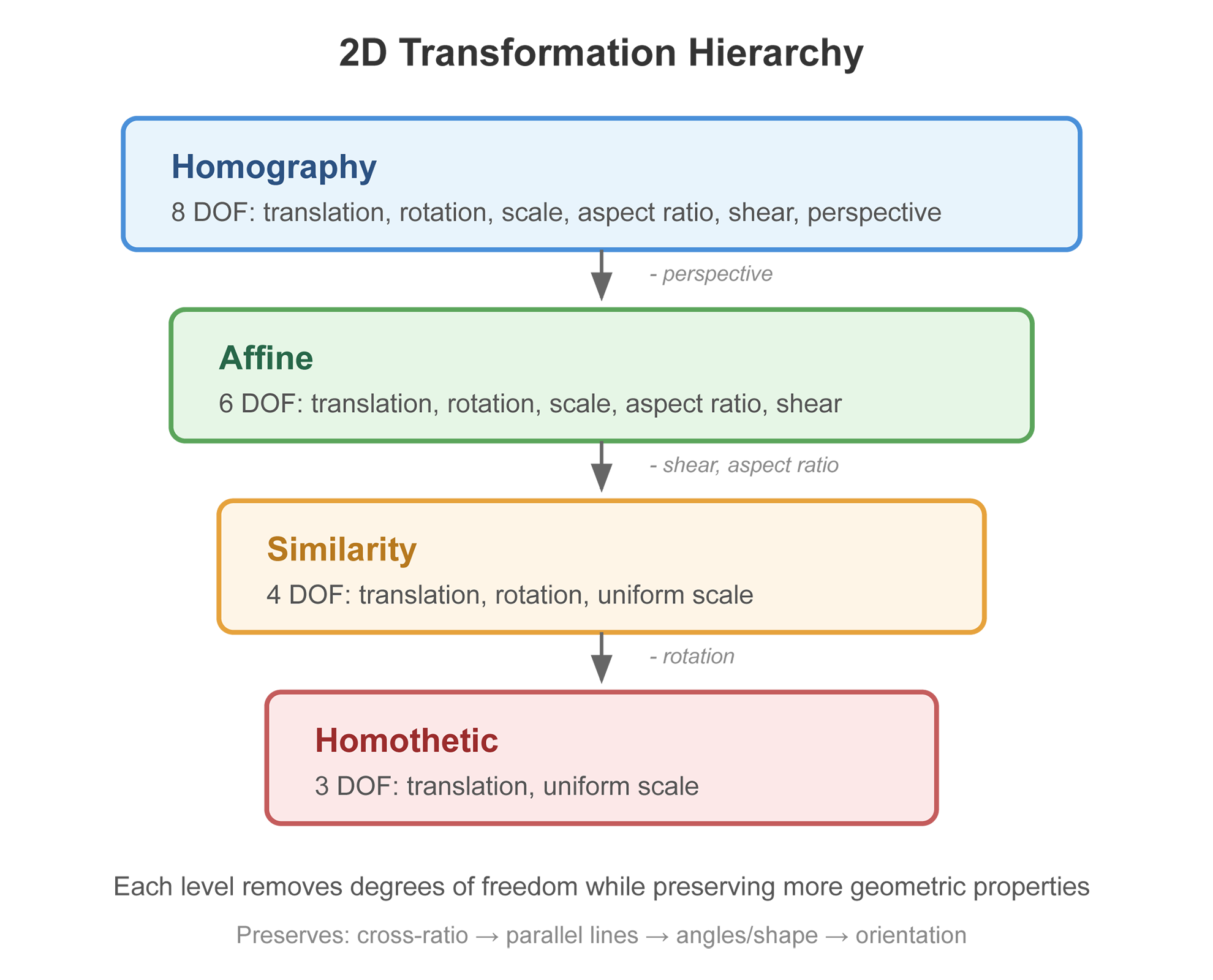
Transformation Hierarchy

Each transformation type is a special case of those above it. Moving down the hierarchy removes degrees of freedom but provides stronger guarantees about what properties are preserved.

Homography Transformation​

A homography is an 8-DOF transformation that includes translation, rotation, scale, aspect ratio, shear, and perspective. It is the most general 2D transformation that maps straight lines to straight lines.

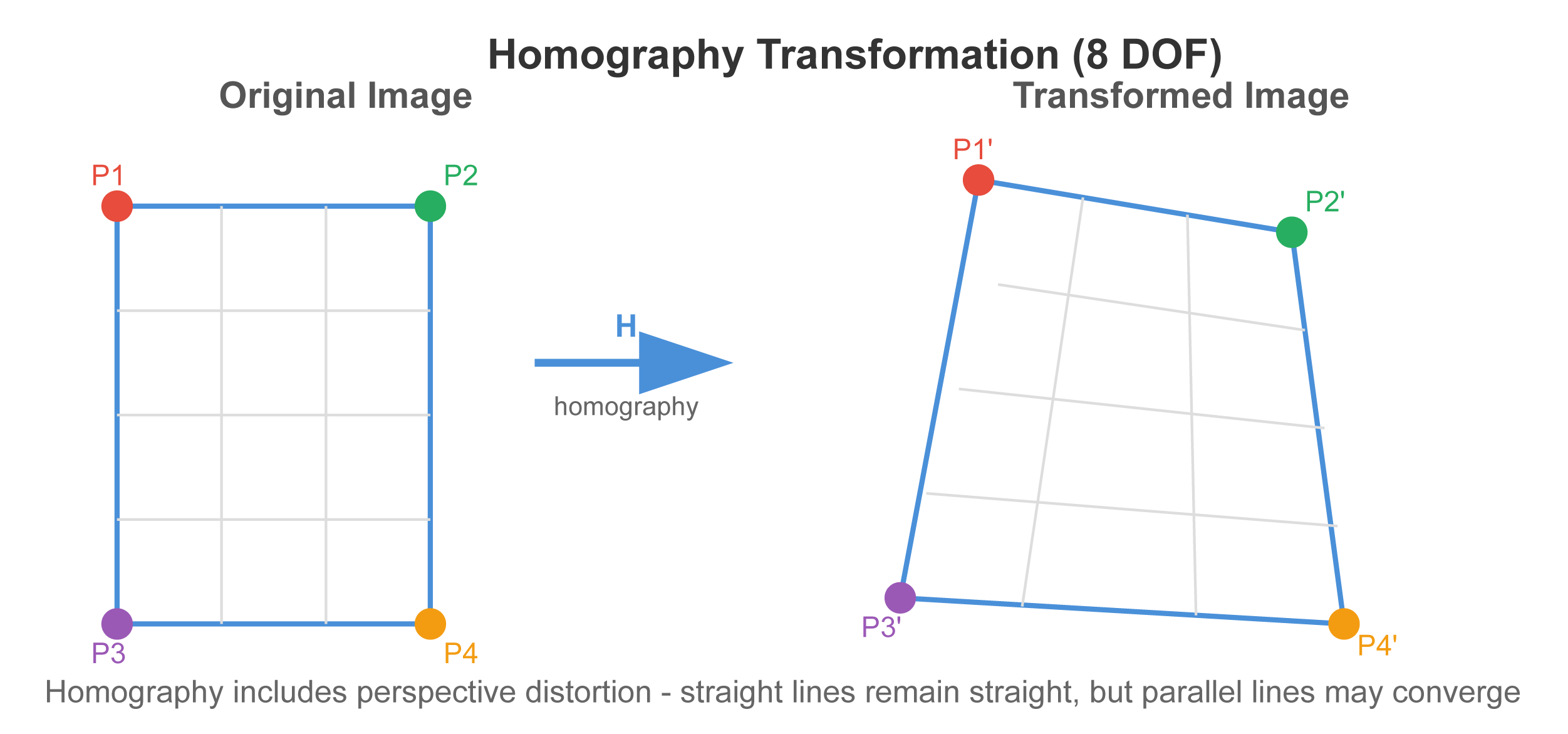
Homography Example

When to Use​

  • Image stitching: Aligning overlapping images into a panorama
  • Perspective correction: Rectifying images of planar surfaces (documents, whiteboards)
  • AR overlays: Projecting content onto planar surfaces in a scene
  • Planar tracking: Following a planar target across video frames

Computing Homographies​

Ocean provides multiple ways to compute homographies depending on your input data:

From 2D Point Correspondences​

The most common approach when you have matched feature points between two images:

#include "ocean/geometry/Homography.h"

// Given matching points in two images
std::vector<Vector2> leftPoints = { /* ... */ };
std::vector<Vector2> rightPoints = { /* ... */ };

SquareMatrix3 right_H_left;
bool success = Geometry::Homography::homographyMatrix(
    leftPoints.data(),
    rightPoints.data(),
    leftPoints.size(),  // minimum 4 correspondences required
    right_H_left,
    true  // use SVD for accuracy (false = faster linear method)
);

if (success)
{
    // Transform a point from left image to right image
    Vector3 leftPointHomogeneous(leftPoint.x(), leftPoint.y(), 1);
    Vector3 rightPointHomogeneous = right_H_left * leftPointHomogeneous;
    Vector2 rightPoint(
        rightPointHomogeneous.x() / rightPointHomogeneous.z(),
        rightPointHomogeneous.y() / rightPointHomogeneous.z()
    );
}

From Camera Rotation​

When you know the relative rotation between two camera views (e.g., from an IMU):

#include "ocean/geometry/Homography.h"

// Rotation from right camera to left camera
Quaternion left_R_right = /* rotation from sensors */;

// Camera profiles
const AnyCamera& leftCamera = /* ... */;
const AnyCamera& rightCamera = /* ... */;

// Compute homography for rotational motion
SquareMatrix3 right_H_left = Geometry::Homography::homographyMatrix(
    left_R_right,
    leftCamera,
    rightCamera
);

From Camera Poses and a Known Plane​

When you have full 6-DOF camera poses and know the 3D plane being imaged:

#include "ocean/geometry/Homography.h"

// Camera poses
HomogenousMatrix4 world_T_leftCamera = HomogenousMatrix4(true);  // identity
HomogenousMatrix4 world_T_rightCamera = /* right camera pose */;

// The plane in world coordinates
Plane3 worldPlane(Vector3(0, 1, 0), 0);  // e.g., ground plane

SquareMatrix3 right_H_left = Geometry::Homography::homographyMatrix(
    world_T_rightCamera,
    leftCamera,
    rightCamera,
    worldPlane
);

Working with Homographies​

Normalizing Homographies​

Homographies are defined up to scale. Normalize to ensure the bottom-right element is 1:

SquareMatrix3 normalizedH = Geometry::Homography::normalizedHomography(right_H_left);

// Or in-place:
Geometry::Homography::normalizeHomography(right_H_left);

Scaling for Different Resolutions​

When images are resized, homographies need to be adjusted:

// If left image was scaled by 0.5 and right image by 2.0
SquareMatrix3 scaledH = Geometry::Homography::scaleHomography(
    right_H_left,
    Scalar(0.5),   // scaleLeft
    Scalar(2.0)    // scaleRight
);

Checking Plausibility​

Verify that a homography represents a valid transformation:

bool isValid = Geometry::Homography::isHomographyPlausible(
    leftImageWidth,
    leftImageHeight,
    rightImageWidth,
    rightImageHeight,
    right_H_left
);

Factorizing into Rotation and Translation​

Extract camera motion from a homography:

HomogenousMatrix4 world_T_rightCameras[2];
Vector3 planeNormals[2];

bool success = Geometry::Homography::factorizeHomographyMatrix(
    right_H_left,
    leftCamera,
    rightCamera,
    leftPoints.data(),
    rightPoints.data(),
    correspondences,
    world_T_rightCameras,
    planeNormals
);

// Two solutions are returned - use scene knowledge to select the correct one

Affine Transformation​

An affine transformation is a 6-DOF transformation that includes translation, rotation, scale, aspect ratio, and shear, but no perspective distortion. Parallel lines remain parallel under affine transformation.

When to Use​

  • Transformations where perspective distortion is negligible (distant objects, near-orthographic views)
  • Texture mapping onto surfaces viewed at moderate angles
  • When you need to preserve parallel line relationships
  • When only 3 point correspondences are available

Computing Affine Transformations​

#include "ocean/geometry/Homography.h"

std::vector<Vector2> leftPoints = { /* ... */ };
std::vector<Vector2> rightPoints = { /* ... */ };

SquareMatrix3 right_A_left;
bool success = Geometry::Homography::affineMatrix(
    leftPoints.data(),
    rightPoints.data(),
    leftPoints.size(),  // minimum 3 correspondences required
    right_A_left
);

if (success)
{
    // Transform points the same way as with homography
    // The bottom row will be [0, 0, 1]
}

Similarity Transformation​

A similarity transformation is a 4-DOF transformation that includes translation, rotation, and uniform scale. It preserves the shape of objects - angles and proportions remain the same.

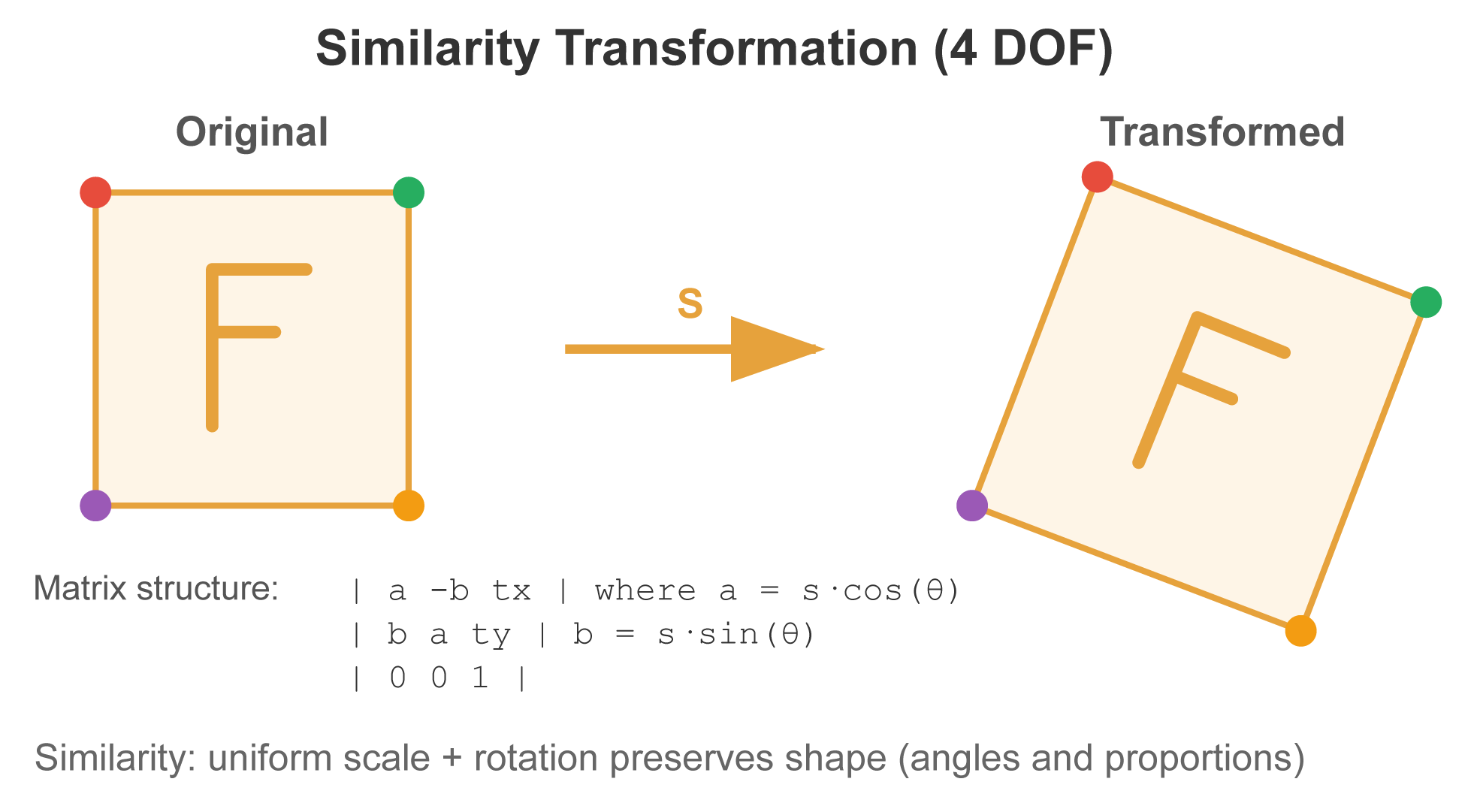
Similarity Example

The similarity matrix has this structure:

| a  -b  tx |
| b   a  ty |
| 0   0   1 |

Where a and b encode rotation and uniform scale, and tx, ty encode translation.

When to Use​

  • Shape-preserving transformations (logos, icons, UI elements)
  • When aspect ratio must be maintained
  • Object tracking where the object doesn't deform
  • When only 2 point correspondences are available

Computing Similarity Transformations​

#include "ocean/geometry/Homography.h"

std::vector<Vector2> leftPoints = { /* ... */ };
std::vector<Vector2> rightPoints = { /* ... */ };

SquareMatrix3 right_S_left;
bool success = Geometry::Homography::similarityMatrix(
    leftPoints.data(),
    rightPoints.data(),
    leftPoints.size(),  // minimum 2 correspondences required
    right_S_left
);

// Extract scale and rotation from the matrix
Scalar scale = Vector2(right_S_left(0, 0), right_S_left(1, 0)).length();
Scalar rotation = Numeric::atan2(right_S_left(1, 0), right_S_left(0, 0));

Homothetic Transformation​

A homothetic transformation is a 3-DOF transformation that includes translation and uniform scale only - no rotation. It preserves both shape and orientation.

The homothetic matrix has this structure:

| s  0  tx |
| 0  s  ty |
| 0  0   1 |

When to Use​

  • Simple scale-and-translate operations
  • When object orientation is known to be fixed
  • UI positioning with size adjustments
  • When you need the simplest transformation model

Computing Homothetic Transformations​

#include "ocean/geometry/Homography.h"

std::vector<Vector2> leftPoints = { /* ... */ };
std::vector<Vector2> rightPoints = { /* ... */ };

SquareMatrix3 right_H_left;
bool success = Geometry::Homography::homotheticMatrix(
    leftPoints.data(),
    rightPoints.data(),
    leftPoints.size(),  // minimum 2 correspondences required
    right_H_left
);

// Extract scale and translation
Scalar scale = right_H_left(0, 0);
Vector2 translation(right_H_left(0, 2), right_H_left(1, 2));

Absolute Transformation​

Absolute transformation computes the rigid transformation (rotation + translation) and optional scale between two sets of 3D points or 6-DOF poses. This is fundamental for aligning coordinate systems in 3D applications.

When to Use​

  • SLAM: Aligning reconstructed maps with ground truth
  • Sensor fusion: Registering data from different sensors
  • Multi-view reconstruction: Aligning partial reconstructions
  • Coordinate system alignment: Converting between different reference frames

Scale Error Types​

Ocean provides three options for computing the scale factor:

TypeDescriptionBest For
RightBiasedMinimizes error in the right coordinate systemWhen right coordinates are the reference
LeftBiasedMinimizes error in the left coordinate systemWhen left coordinates are the reference
SymmetricSymmetric formulation (recommended by Horn)General case, no preference

Computing Absolute Transformations​

From 3D Point Correspondences​

#include "ocean/geometry/AbsoluteTransformation.h"

std::vector<Vector3> leftPoints = { /* 3D points in left coordinate system */ };
std::vector<Vector3> rightPoints = { /* corresponding points in right system */ };

HomogenousMatrix4 right_T_left;
Scalar scale = 0;

bool success = Geometry::AbsoluteTransformation::calculateTransformation(
    leftPoints.data(),
    rightPoints.data(),
    leftPoints.size(),  // minimum 3 correspondences required
    right_T_left,
    Geometry::AbsoluteTransformation::ScaleErrorType::Symmetric,
    &scale
);

if (success)
{
    // Apply scale to the transformation if needed
    right_T_left.applyScale(Vector3(scale, scale, scale));

    // Transform a point from left to right coordinate system
    Vector3 rightPoint = right_T_left * leftPoint;
}

From 6-DOF Pose Correspondences​

When aligning trajectories or sets of camera poses:

#include "ocean/geometry/AbsoluteTransformation.h"

std::vector<HomogenousMatrix4> leftPoses = { /* poses in left world */ };
std::vector<HomogenousMatrix4> rightPoses = { /* corresponding poses in right world */ };

HomogenousMatrix4 rightWorld_T_leftWorld;
Scalar scale = 0;

bool success = Geometry::AbsoluteTransformation::calculateTransformation(
    leftPoses.data(),
    rightPoses.data(),
    leftPoses.size(),  // minimum 1 correspondence, more is better
    rightWorld_T_leftWorld,
    Geometry::AbsoluteTransformation::ScaleErrorType::Symmetric,
    &scale
);

if (success)
{
    // Transform all poses from left world to right world
    for (const auto& leftPose : leftPoses)
    {
        HomogenousMatrix4 rightPose = rightWorld_T_leftWorld * leftPose;
        rightPose.applyScale(Vector3(scale, scale, scale));
    }
}

Handling Outliers​

For data that may contain incorrect correspondences:

HomogenousMatrix4 rightWorld_T_leftWorld;
Scalar scale = 0;

bool success = Geometry::AbsoluteTransformation::calculateTransformationWithOutliers(
    leftPoses.data(),
    rightPoses.data(),
    leftPoses.size(),
    rightWorld_T_leftWorld,
    Scalar(0.75),  // expected inlier rate (75%)
    Geometry::AbsoluteTransformation::ScaleErrorType::Symmetric,
    &scale
);

Choosing the Right Transformation​

Use this decision guide to select the appropriate transformation:

Do you have 3D data?

  • Yes → Use AbsoluteTransformation
  • No → Continue below

Is there perspective distortion?

  • Yes (objects at varying depths, camera tilted relative to plane) → Use Homography
  • No → Continue below

Are there shear or aspect ratio changes?

  • Yes → Use Affine
  • No → Continue below

Is there rotation?

  • Yes → Use Similarity
  • No → Use Homothetic

How many point correspondences do you have?

  • 4+ reliable points → Homography is possible
  • 3 reliable points → Use Affine maximum
  • 2 reliable points → Use Similarity or Homothetic

Normalization Helpers​

The Geometry::Normalization class provides utilities for normalizing points before computing transformations, which can improve numerical stability:

#include "ocean/geometry/Normalization.h"

std::vector<Vector2> points = { /* ... */ };

// Normalize points so RMS distance from origin is sqrt(2)
SquareMatrix3 points_T_normalizedPoints;
SquareMatrix3 normalizedPoints_T_points = Geometry::Normalization::calculateNormalizedPoints(
    points.data(),
    points.size(),
    &points_T_normalizedPoints  // optional inverse transformation
);

// After computing transformation with normalized points,
// denormalize the result:
// H = points_T_normalizedPointsRight * H_normalized * normalizedPoints_T_pointsLeft

Resources​